Большое спасибо всем, кто помогает делать сайт лучше! =)
Все матерные комментарии (даже восторженные) – удаляются.Если хотите получить решение,- спрашивайте не в комментариях, а на .
Не знаете как решить? Можете помочь с решением? Заходите .Или , качественно, скидка от 5terka.com 5% по купону WW623296
Аналогично устанавливается параллельность прямых В1С1 и Так что А1В1С1В1 параллелограмм. Что и требовалось доказать.
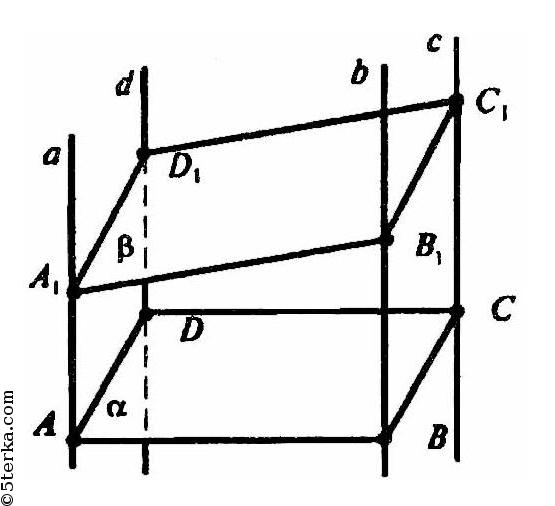
Пусть другая плоскость пересекает эти прямые в точках А1, В1, С1, D1 соответственно. плоскости αВВ1А1 и CDD1C1, параллельны, поскольку прямые АВ и CD, и прямые а и d параллельны. А, значит, плоскость β пересекает эти плоскости по параллельным прямым А1В1 и C1D1.
Пусть а, b, с, d данные прямые, и плоскость α пересекает эти прямые в вершинах параллелограмма ABCD.
→ номер 36
W 16. Параллельность прямых и плоскостей
Онлайн решебник
36. Даны четыре параллельные прямые. Докажите, что если какая-нибудь плоскость пересекает эти прямые в вершинах параллелограмма, то любая плоскость, не параллельная этим прямым, пересекает их в вершинах некоторого параллелограмма. | Решение на пятёрке!
Комментариев нет:
Отправить комментарий